Six Stages Of Debugging

The 21 Card Trick created in Python.

See how it works and read a little more about it here: [x]

Feel free to ask any questions you may have. :)

That’s the secret of programming.

How to draw a regular pentagon [x]

Regarding Fractals and Non-Integral Dimensionality

Alright, I know it’s past midnight (at least it is where I am), but let’s talk about fractal geometry.

Fractals

If you don’t know what fractals are, they’re essentially just any shape that gets rougher (or has more detail) as you zoom in, rather than getting smoother. Non-fractals include easy geometric shapes like squares, circles, and triangles, while fractals include more complex or natural shapes like the coast of Great Britain, Sierpinski’s Triangle, or a Koch Snowflake.

Fractals, in turn, can be broken down further. Some fractals are the product of an iterative process and repeat smaller versions of themselves throughout them. Others are more natural and just happen to be more jagged.

Fractals and Non-Integral Dimensionality

Now that we’ve gotten the actual explanation of what fractals are out of the way, let’s talk about their most interesting property: non-integral dimensionality. The idea that fractals do not actually have an integral dimension was originally thought up by this guy, Benoit Mandelbrot.

He studied fractals a lot, even finding one of his own: the Mandelbrot Set. The important thing about this guy is that he realized that fractals are interesting when it comes to defining their dimension. Most regular shapes can have their dimension found easily: lines with their finite length but no width or height; squares with their finite length and width but no height; and cubes with their finite length, width, and height. Take note that each dimension has its own measure. The deal with many fractals is that they can’t be measured very easily at all using these terms. Take Sierpinski’s triangle as an example.

Is this shape one- or two-dimensional? Many would say two-dimensional from first glance, but the same shape can be created using a line rather than a triangle.

So now it seems a bit more tricky. Is it one-dimensional since it can be made out of a line, or is it two-dimensional since it can be made out of a triangle? The answer is neither. The problem is that, if we were to treat it like a two-dimensional object, the measure of its dimension (area) would be zero. This is because we’ve technically taken away all of its area by taking out smaller and smaller triangles in every available space. On the other hand, if we were to treat it like a one-dimensional object, the measure of its dimension (length) would be infinity. This is because the line keeps getting longer and longer to stretch around each and every hole, of which there are an infinite number. So now we run into a problem: if it’s neither one- nor two-dimensional, then what is its dimensionality? To find out, we can use non-fractals

Measuring Integral Dimensions and Applying to Fractals

Let’s start with a one-dimensional line. The measure for a one-dimensional object is length. If we were to scale the line down by one-half, what is the fraction of the new length compared to the original length?

The new length of each line is one-half the original length.

Now let’s try the same thing for squares. The measure for a two-dimensional object is area. If we were to scale down a square by one-half (that is to say, if we were to divide the square’s length in half and divide its width in half), what is the fraction of the new area compared to the original area?

The new area of each square is one-quarter the original area.

If we were to try the same with cubes, the volume of each new cube would be one-eighth the original volume of a cube. These fractions provide us with a pattern we can work with.

In one dimension, the new length (one-half) is equal to the scaling factor (one-half) put to the first power (given by it being one-dimensional).

In two dimensions, the new area (one-quarter) is equal to the scaling factor (one-half) put to the second power (given by it being two-dimensional).

In three dimensions, the same pattern follows suit, in which the new volume (one-eighth) is equivalent to the scaling factor (one-half) put to the third power.

We can infer from this trend that the dimension of an object could be (not is) defined as the exponent fixed to the scaling factor of an object that determines the new measure of the object. To put it in mathematical terms:

Examples of this equation would include the one-dimensional line, the two-dimensional square, and the three-dimensional cube:

½ = ½^1

¼ = ½^2

1/8 = ½^3

Now this equation can be used to define the dimensionality of a given fractal. Let’s try Sierpinski’s Triangle again.

Here we can see that the triangle as a whole is made from three smaller versions of itself, each of which is scaled down by half of the original (this is proven by each side of the smaller triangles being half the length of the side of the whole triangle). So now we can just plug in the numbers to our equation and leave the dimension slot blank.

1/3 = ½^D

To solve for D, we need to know what power ½ must be put to in order to get 1/3. To do this, we can use logarithms (quick note: in this case, we can replace ½ with 2 and 1/3 with 3).

log_2(3) = roughly 1.585

So we can conclude that Sierpinski’s triangle is 1.585-dimensional. Now we can repeat this process with many other fractals. For example, this Sierpinski-esque square:

It’s made up of eight smaller versions of itself, each of which is scaled down by one-third. Plugging this into the equation, we get

1/8 = 1/3^D

log_3(8) = roughly 1.893

So we can conclude that this square fractal is 1.893-dimensional.

We can do this on this cubic version of it, too:

This cube is made up of 20 smaller versions of itself, each of which is scaled down by 1/3.

1/20 = 1/3^D

log_3(20) = roughly 2.727

So we can conclude that this fractal is 2.727-dimensional.

Geometry and Divnity

Omnipresence

The Point

Divinity is present in every aspect of natural order and causality dimensions. It is part of the material world through various holistic and messianic incarnations, being at the same time a component of human thought and action. This kind of omnipresence is logical possible through the classical definition of a geometrical point, that is part of the entire space but does not occupy any of it.

Trinity

The Borromean Rings

While distinct and at the same time considered to be one in all else, the Three Divine Persons are sometimes represented by the Borromean Rings: no two of the three rings are linked with each other,but nonetheless all three are linked.

Divinity

Harmonic Proportion

The harmonic state of an element is associated with beauty, given by the equilibrium of its components. Nature is being perceived as beautiful, and its creator as good - inevitable and inherently in harmony with its creation.

Programmer LoGiC

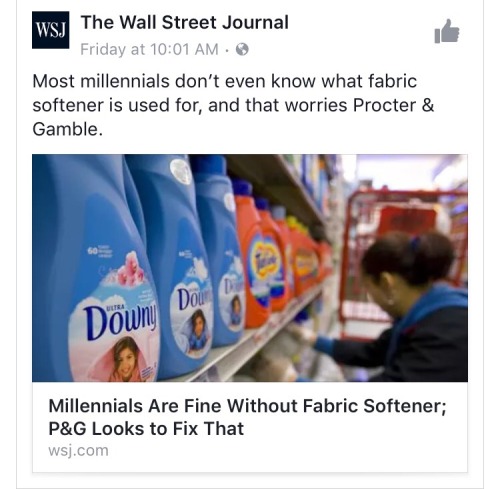
Weirdly anti-millennial articles have scraped the bottom of the barrel so hard that they are now two feet down into the topsoil

Everyone who reblogs this will get a pick-me-up in their ask box.

Every. Single. One. Of. You.

A sand pendulum that creates a beautiful pattern only by its movement.

But  why does the ellipse change shape?

The pattern gets smaller because energy is not conserved (and in fact decreases) in the system. The mass in the pendulum gets smaller and the center of mass lowers as a function of time. Easy as that, an amazing pattern arises through the laws of physics.